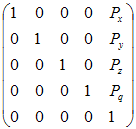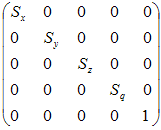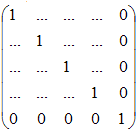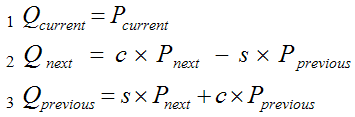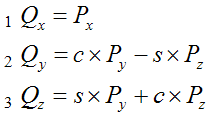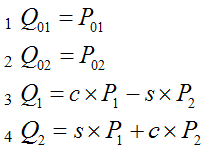 |
 |
|
|
|
|
|
|
|
3. Математика 3.2 Четырехмерные аффинные преобразования |
|
Для начала советую ознакомится с главами Матрицы, Аффинные преобразования и Трехмерные аффинные преобразования |
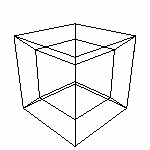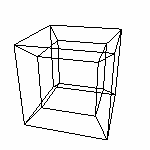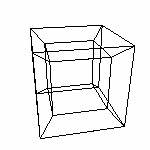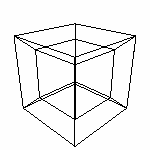
| Четырехмерные
аффинные преобразования - те же, что и уже рассмотренные и
их матрицы можно получить логическим путем. Просто матрицы будут
пять на пять. Перемещение просто и легко
Масштабирование - от туда же
Сдвиг - вместо многоточий какие-нибудь коэффициенты.
Но не все так просто... Поворот Вот тут начинаются танцы с бубнами вокруг
пионерского костра. Сначала определимся. Но на самом деле (исходя из смысла понятия вращение) главным и определяющим является совокупность осей, которые лежат в плоскости вращения, и их порядок указывает направление вращения (например от x-к y). А вот вокруг чего производится поворот - это не важно. Пионерский костер зажгли. Но ведь я Вам обещал танцы. Для этого понадобится пара бубнов. Их есть у меня.
Бубен №1. |
| 3D | 4D | ||
| Определение | Матрица | Определение | Матрица |
| Вокруг x от y к z |
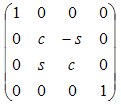 |
Вокруг xq от y к z |
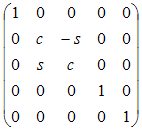 |
| Вокруг y от z к x |
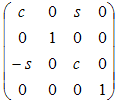 |
Вокруг yq от z к x |
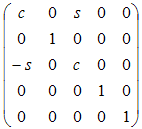 |
| Вокруг z от x к y |
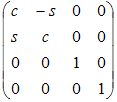 |
Вокруг zq от x к y |
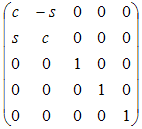 |
|
Как же получить другие вращения? Для 3D-матриц у нас было два способа логического нахождения матриц. Сразу скажу, что способ со смещением строк и столбцов не совсем подходит (предлагаю вам проверить это самим). Да и способ с тремя уравнениями не совсем нам подходит. Но после небольшой модификации будет в самый раз. А пока... Бубен №2 Сей артефакт закопан недалеко от поверхности. Сейчас откопаем, приватизируем и будем пляски танцевать. Если присмотреться внимательнее к матрицам аффинных преобразований определяющих вращение и их определениям, то можно заметить, что расположение значимых элементов и определение матрицы связано следующим образом (в принципе следующий вывод напрашивается сам собой, если разобраться с самой сущностью понятия вращение, но на матрицах нагляднее). Из пояснения каким образом матрица описывает преобразование можно сделать вывод, что в матрице вращения коэффициенты стоят в тех строках (и столбцах), которые указывают на оси в плоскости вращения, а строки (и столбцы) без коэффициентов на то, вокруг чего идет вращение. Косинусы всегда на диагонали, а синусы в двух других углах воображаемого квадрата. Также с помощью нехитрых умозаключений сделаем вывод, что строка (но не столбец) с минусом определяет первую ось в направлении вращения (от которой), а строка без минуса вторую ось (к которой). Со столбцами наоборот.. Таким образом можно получить любые матрицы на заказ. Рассмотрим таблицу. В каждой строке определяются всевозможные параметры вращения. В последнем столбце матрица, полученная с помощью только что полученного вывода.
|
| Вокруг чего | От чего | К чему | Матрица |
| xy | z | q |
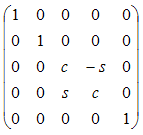 |
| xz | q | y |
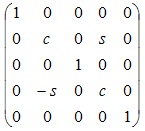 |
| xq | y | z |
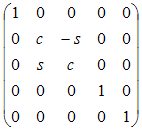 |
| yz | q | x |
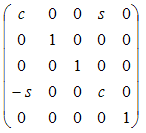 |
| yq | z | x |
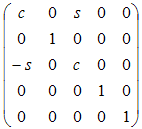 |
| zq | x | y |
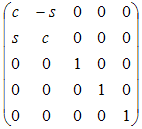 |
| Конечно Вы можете и не
согласится со взятыми направления поворота (от ... к ...) но тут
нечего не поделаешь. Дело вкуса. Обобщим. Существует, на этот раз не циклическая последовательность осей x, y, z, q. И для элементов этой последовательность есть понятия меньше-больше (в зависимости от расположения в порядке следования x<y<z<q) Тогда схема матрицы для вращения в направлении от Оси1 к Оси2. Если Ось1 меньше, чем Ось2, то минус стоит у верхнего (правого) синуса. Если Ось1 больше, чем Ось2, то минус стоит у нижнего (левого) синуса Как видите тут даже нет упоминания про то, вокруг чего поворачиваем. Это еще одно доказательство того, что вращение происходит не "вокруг чего-то", а "от...к..." Это подтверждается и вот этой формулой (3.1) Только в ней система названий не подходит к нашему случаю. Давайте разберемся. Для начала напомню ее
где "текущий", "следующий" и "предыдущий" - это обобщающие названия координат (по названию осей) рассматриваемой в циклической последовательности x→y→z→ x→y,… и т.д. При этом "текущей" берется та, которая определяет ось, вокруг которой происходит поворот. Поясню на примере, когда текущий - x.
В нашем случае поворот происходит вокруг плоскости. А ведь как мы выяснили при построении модели четырехмерного пространства в этом пространстве нет последовательности плоскостей. И поэтому нет "предыдущей" и "следующей". Поэтому нам надо изменить систему названий. Назовем 01 и 02 - оси, определяющие плоскость, вокруг которой происходит вращение. А также: 1 - первая ось в последовательности направления (от которой) 2 - вторая ось (к которой) Тогда получаем
В файлах моделирования трехмерной проекции четырехмерного объекта, направления поворота берутся в таком виде: xy, xz, xq, yz, yq, zq. Но существует определенные проблемы с реализацией вращения в программах моделирования. Подробности в следующей статье. |
|
|
|
|
|
|
|
©2007 AnCoRecords "d'Amateur: Записки 4D любителя" E-mail автору |
|
|
|