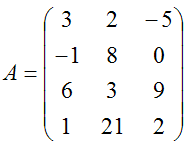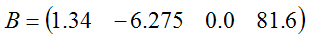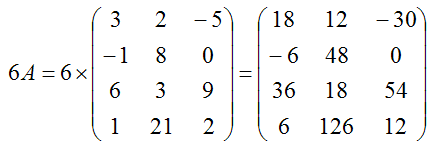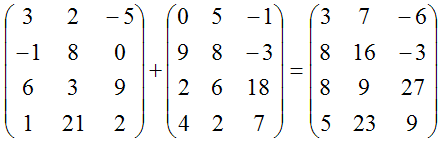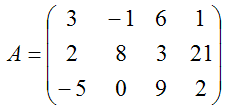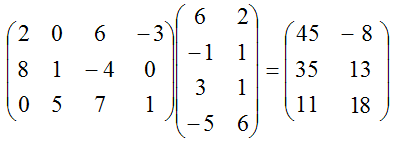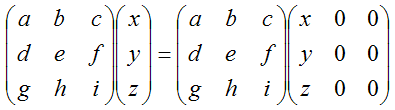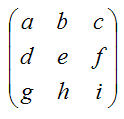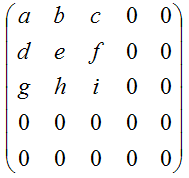4.1 Матрицы

Matrix. Revolution.

  При использовании [Л1].

  В данном приложении делается обзор некоторых фундаментальных понятий, относящихся к матрицам, а также действия с матрицами. Другие операции над матрицами можно найти в посвященных им изданиях.

Матрица (matrix) - это прямоугольный массив элементов, чаще всего чисел. Матрицу, имеющую m строк и n столбцов, матрицей размерностью m на n (в некоторых источниках размерность называют структурой матрицы). (обозначается m×n). Например,

это матрица целых чисел размерностью 4 на 3, а матрица

это матрица один на 4, также называемая "четверкой" ("quadruple") или вектором. Обычно матрицу размерностью одина на n называют "вектором-строкой" (row vector), а матрицу размерностью n на один  "вектором-столбцом" (column vector).

  Отдельные элементы матрицы обычно обозначаются строчными буквами с различными нижними индексами: ij--й элемент матрицы B обозначается b_ij. Это элемент i-й строки и  j-го столбца. Например, для матрицы  A из уравнения (M4.1.1) элемент a₃₂=3.

  Матрица называется квадратной (square), если число ее строк и столбцов одинаково. В данном проекте мы часто имеем дело с матрицами размерностью два на два, три на три, четыре на четыре, а также для четвертого измерения матрица пять на пять. Часто используются следующие два вила матриц: нулевая матрица (zero matrix) и "единичная матрица" (identity matrix). Все элементы нулевой матрицы равны нулю. У единичной матрицы равны нуля все элементы, за исключением элементов главной диагонали. (main diagonal) a_ij (у которых i=j), которые равны единице. Следовательно единичная матрица три на три имеет вид:

  4.1.1 Действия над матрицами

  Числовая матрица B может быть масштабирована (scaled) числом s (умножена на число  s). При этом каждый элемент матрицы  умножается на s. Полученная матрица обозначается sB. К примеру, для матрицы A из уравнения (M4.1.1) получим:

  Дви матрицы C и D, имеющие одинаковое число строк и столбцов, называются матрицами одинаковой размерности (shape), и их можно складывать. Элемент ij этой суммы E=C+D является просто суммой соответствующих элемент e_ij=c_ij+d_ij. Например,

  Поскольку матрицы можно масштабировать и складывать, имеет смысл определить линейный комбинации (linear combinations) матриц (одинаковой размерности), например 2A-4B. Из определений сложения и масштабирования непосредственно следуют свойства коммутативности, ассоциативности и дистрибутивности для трех матриц A, B, C одинаковой размерности:

A+B=B+A

A+(B+C)=(A+B)+C

(f+g)(A+B)=fA+fB+gA+gB.

  Результат транспонирования (transpose) матрицы M, обозначаемый M^T, образуется посредством перестановки (взаимной замены) строк и столбцов матрицы M: ij-й  элемент матрицы M^T равен ji-му элементу матрицы M. Например, транспонирование матрицы A из уравнения (M4.1.1) дает:

  Результатом транспонирования вектора-строки является вектор-столбец. Например,

Матрица называется симметричной (symmetric), если она не изменяется при транспонировании. Симметричными могут быть только квадратные матрицы. Таким образом, матрица M размерностью n×n является симметричной, если m_ij=m_ji для всех i и j от 1 до n.

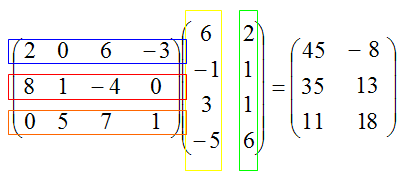
 4.1.1 Умножение двух матриц

  В разделе Математика рассматриваются преобразования, включающие в себя умножение вектора на матрицу и умножение двух матриц друг на друга. Пераое понятие явлется частным случаем второго.

  Произведение (product) AB двух матриц A и B определено только в том случае, если эти две матрицы являются согласованными (conform). Это означает, что число столбцов первой матрицы A равно числу строк второй матрицы матрицы B. Таким образом, если матрица A имеет размерность 3×5, а матрица B - 5×2, то произведение AB определено, а произведение BA - нет. Каждый элемент произведения C матриц A и B C=AB является скалярным произведением некоторой строки матрицы A на некоторый столбец матрицы B. А именно, ij-й элемент с_ij этого произведения является скалярным произведением i-й строки матрицы A на j-й столбец матрицы B. Тогда произведение матрицы размерностью m×n на матрицу размерностью n×r будет матрица m×r. Пример:

Проще говоря мы получаем элемент путем суммы произведений соответствующих элементов

с_{11=     *}        с_{12=     *}   

с_{21=     *}        с_{22=     *}   

с_{31=     *}        с_{32=     *}   

Файл MS Excel с таблицей расчета произведений матриц в текстовом и числовом вариантах.

  Перечислим некоторые полезные свойства умножения матриц. Пусть матрицы A, B, C согласуются должным образом. Тогда

(AB)C=A(BC)

A(B+C)=AB+AC

(A+B)C=AC+BC

(AB)^T=B^TA^T

A(sB)=sAB,

где s - число.

  При формировании произведения двух матриц A и B имеет значение порядок следования матриц. О выражении AB мы говорим : "A умножается слева (premultiplies) на B" или "B умножается справа (postmultiplied) на A". Если обе матрицы квадратные и одной и той же размерности, то оба произведения - AB и BA - определены, однако эти два произведения могут содержать различные элементы. Если для двух матриц AB=BA, то эти две матрицы называются коммутативными (commute).

  Частным случаем умножения матриц является случай, когда одна из матриц является вектором-строкой или вектором-столбцом. В Аффинных преобразованиях используется именно умножение справа вектора-столбца (определяющий координаты точки) на матрицу преобразования. Рассматривать его нет необходимости, потому что, для всех расчетов в теме данного проекта можно использовать следующее

и вообще

заменять при необходимости например на

Эти матрицы разные, но для понимания сути в контексте всего проекта это в самый раз.

  Были перечислены те понятия, которые используются в разделе Математика. Более полное описание свойств и взаимоотношений матриц ищите в специализированных статьях.