Назад Четырехмерные аффинные преобразования

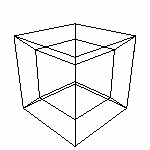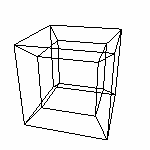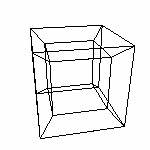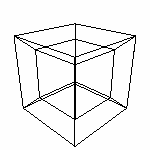
Далее Построение куба

3.7 Проблема с вращением

Существует определенная проблема с реализацией вращения в программах визуализации.

Дело в том, что, как уже говорилось, аффинные преобразования не коммутативны. При изменении порядка - получим другой результат. то же относится к вращению.

Рассмотрим два последовательных вращения. Первый на угол α, второй на угол β.

От x к y,  и после от y к z.

Допустим точка лежит на оси x.

Первый поворот...

(П1)

и второй поворот.

(П2)

Получаем точку с ненулевыми x,y,z - координатами.

Рассмотрим последовательность наоборот.

От y к z  - это означает вращение вокруг оси x

(П3)

Точка осталась на оси. Она ведь лежит на оси, вокруг которой мы ее вращаем.

После этого поворот от x к y.

(П4)

Как видно, результат (П4) отличается от предыдущего (П2).

А как же поворачивать во всех направлениях одновременно?

В программах трехмерного моделирования на этом сайте реализована возможность указывать углы поворотов сразу в  нескольких (а, конкретно, в шести) направлениях (имеется в виду в четырех мерном пространстве).

И там эта проблема существует.

При указании параметров - угла и коэффициентов xy,xz,xq,yz,yq,zq - последовательность поворотов в каждом направлении происходит именно в этом порядке. То есть точка (и объект) поворачивает не сразу на один угол учитывая все коэффициенты, а по порядку сначала от x к y, потом от x к z и т.д. И поэтому при указании всех коэффициентов конечная точка не совсем то, что получилось бы при одновременном повороте.(это очень хорошо видно на примерах в конце статьи). Если Вам необходимо реализовать повороты в другом порядке, используйте несколько вращений в нужном порядке.

Например,

Поворот (0 0 0 0 1 0)

Поворот (1 0 0 0 0 0)

Эта последовательности сначала произведет поворот yq, а потом xy.

А вот если написать так

Поворот (1 0 0 0 1 0)

то это аналогично повороту xy , а потом yq.

  В трехмерном пространстве это реализуется довольно-таки легко, используя теорему Эйлера (см [М3] [М4]).

Далее по [Л1]

Теорема Эйлера.

Любой поворот (или последовательность поворотов) вокруг произвольной точки эквивалентен однократному повороту вокруг некоторой оси, проходящей через эту точку.

Иногда эта теорем формулируется так.

Если заданы две прямоугольные системы координаты с общим началом и произвольным направлением осей, то всегда существует такая прямая, проходящая через начало координат, что одна система координат может быт совмещена с ругой посредством поворота вокруг этой прямой.

Что же представляет собой матрица такого поворота?

Есть два способа получить эту матрицу

Классический способ. Разбиваем искомый поворот на последовательность знакомых шагов

1. Выполним два поворота таким образом, чтобы вектор u совместился с осью x.

2. Вы полним вращение от x к y (трехмерное z-вращение)

3. Аннулируем два совмещающих поворота для восстановления исходного направления вектора u.

(П5)

Этот метод напоминает поворот вокруг точки в двух измерениях. Первый шаг подготавливает условия для более простой и знакомой операция, затем эта простая операция выполняется, и, наконец подготовительный этап аннулируется. Результат для трехмерного случая заключается в том, что нужное преобразования требует перемножения пяти матриц.

//Примечания d'Amateur:  

1. Напоминаю, рассматривать последовательность перемножения матриц необходимо в обратном порядке: самое первое преобразования - на последнем месте.

2. В классическом трехмерном вращении принято рассматривать поворот в направлении zx, поэтому у угла θ знак минус, в отличие от определений в проекте d'Amateur, стоит на других местах, противоположных принятым здесь.//

Каждое умножение является поворотом вокруг одной из координатных осей. Такое преобразование является громоздким для выполнения вручную, однако удобен для воплощения в компьютерной программе. В то же время раскрытие произведения дает мало представления от том , как эти "ингредиенты" работают совместно.

Конструктивный способ. Используя некоторые векторные инструменты, можно получить более наглядное выражение для матрицы R_u(β). В последнее время этот подход стал весьма популярен, и различные его варианты описаны несколькими вторами в GEMS I. Мы используем вывод Мэйллота (Maillot). (см [М1])

  (П6)   

На рисунке (П6) показана ост вращения u, и нам нужно написать выражение для операции перехода точки P в точку Q с помощью поворота на угол β. В данном методе в плоскости вращения устанавливается двумерная система координат, как показано на рисунке. В этой системе координат два ортогональных вектора a и b располагаются в этой плоскости и, как показано на рисунке (П7)

(П7)

точка Q выражается линейной комбинацией этих двух векторов. Выражения для Q включает в себя скалярные и векторные произведения различных "ингредиентов", зависящих от специфики задачи. Однако, поскольку каждый член линеен относительно координат точки P, он может быть записан как произведение матрицы на P.

   Окончательным результатом является матрица

(П8)

 (см [М2])

где c=cosβ, s=sinβ a x,y,z - компоненты единичного вектора u.

Конец цитирования [Л1].

Примечание d'Amateur. Эта матрица для классического направления поворотов. В случае направления поворота вокруг оси y в направлении xz, как принято на этом проекте, в этой матрице необходимо заменить y на (-y).

Так вот, используя (П8) можно реализовать"красивый" трехмерный поворот, когда происходит одновременное вращение во всех трех плоскостях. Скорее всего так и сделано в OpenGL.

Поворот на угол  1 градус одновременно вокруг всех осей с коэффициентами kx,ky,kz соответственно эквивалентен повороту на 1 градус вокруг вектора (kx,ky,kz). Необходимо помнить, что вектор должен быть единичны, то есть длина=1.

Это делается просто

Пример, как различаются одновременный поворот во всех направлениях и последовательный поворот в трехмерном случае можно посмотреть здесь.

Как видите, разница налицо.

Но как реализовать одновременный поворот в шести направлениях четырехмерного пространства я еще пока не решил (не нашел). Поэтому при указании поворотов в списке аффинных преобразований для программ семейства Transformator4D учтите информацию из этой статьи. Эта программа создана не для создания графического движка, а для просмотра проекций четырехмерных фигур. А с этой задачей можно справиться и без "правильных поворотов".

Но обещаю, что как только найду решение этой проблемы, сразу сообщу.

Назад Четырехмерные аффинные преобразования

Далее Построение куба

©2007 AnCoRecords   "d'Amateur: Записки 4D любителя"    E-mail автору