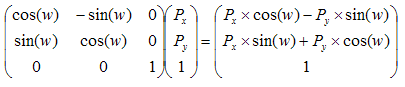4.2 Аффинные преобразования

Вот!
Новый поворот.
И мотор ревет.
Что он нам несет?
Пропать или взлет?
Омут или брод?
И не разберешь,
Пока не повернешь
За поворот.

  Начну с того, аффинные преобразования являются краеугольным камнем всей компьютерной графики. С помощью матриц, как компактного и удобного способа записи преобразований, можно описать все, что происходит с точками, и, соответственно, с объектами, состоящих из этих точек.  На вопросы «почему?», «откуда?» и «зачем?» отвечу лишь: «Обращайтесь к специализированным ресурсам по компьютерной графике…» (например [Л1] или [М1]).
А здесь будем использовать готовые решения.

Основы

Преобразование M точки T(x,y,z), где

является произведение

  Из определения произведения матриц можно сделать вывод о влиянии каждого элемента матрицы преобразования на конечный результат. 

1. Номер строки преобразования определяет изменение соответствующей координаты (первая строка определяет x, вторая y, третья z)

2. Номер столбца определяет способ влияния соответствующей координаты на другие.

(первый столбец определяет влияние координаты x на другие, соответственно номеру строки, второй - как влияет y, третий - z).

3. Последний (в данном случае четвертый) столбец определяет смещение соответствующей координаты на определенную величину.

4. Почему в трехмерном пространстве используется матрица четыре на четыре? Ну на пример, четвертый столбец дает возможность реализовать Перемещение. А в общем случае, такая форма записи является необходимой, так как матрица 4 на 4 целиком используется в проекционных преобразованиях.

Основные виды двумерных аффинных преобразований и их схематическое представление.

4.2.0 Единичная матрица

Основная. Результат преобразования равен оригиналу. Все дело в единицах по диагонали.

4.2.1 Перемещение - перемещает объект

4.2.2 Масштабирование - изменяет размер

4.2.3 Сдвиг - изменение одной координаты в линейной зависимости от другой

4.2.4 Поворот - Поворачивает на угол w

Все преобразования, кроме перемещения, выполняются относительно начала координат.

Сравните результаты одного и того же преобразования при различных положениях объекта.

Масштабирование.

1. Объект начале координат.

масштабируем...

2. Объект не в начале координат

масштабируем...

Объект сместился.

Поворот

1. Объект в начале координат.

поворачиваем...

2. Объект не вначале координат

поворачиваем...

Первые три вида довольно таки простые. А вот "за поворотом" нас ждут много интересных вешчей!

Можно применять несколько преобразований последовательно. Имеет смысл порядок преобразований. (произведение матриц не коммутативно)

Например (помните! все поворот, масштабирование, сдвиг приводятся относительно начала координат)

R - вращение (Rotate), T - перемещение (Transpose).

Сначала перемещаем, потом поворачиваем ...

или поворачиваем, потом перемещаем...

Для преобразования точки необходимо умножить матрицу Точки слева на матрицу преобразования. Для последовательного применения преобразований к точке необходимо по порядку умножать на матрицу слева.

Например, Точка P. Преобразования S,R₁,T,R₂ необходимо

перемножить матрицы следующим образом

 R₂×T×R₁×S×P. А вот разницы в каком порядке перемножать нет

(R₂×T)×(R₁×S)×P или (R₂×T)×(R₁×(S×P)) или другим способом...

Вообще можно сначала подготовить преобразование а потом применять его к точке, то есть найти G=R₂×T×R₁×S, а потом G×P.

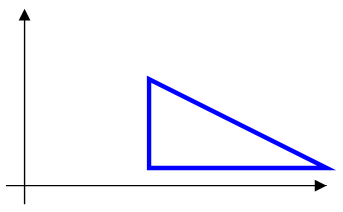
Для тех кто в OpenGL.

  Если программировать модель используя OpenGL и применять последовательно преобразования вращения, перемещения, масштабирования используя инструменты OpenGL glRotated(), glTranspose() и glScaled() и  то результат будет совершенно противоположный чем мы сейчас описали. Дело в том, что в OpenGL преобразования применяются к системе координат, а мы применяем к объекту.

1. Рассмотрим последовательность Поворот->Перемещение

1.1 OpenGL. Преобразование системы координат - Поворачиваем систему координат от x к y, и переносим ее параллельно x', рисуем объект.

Результат - треугольник наклонен и вверху.

1.2 Преобразование объекта. Поворачиваем объект от x к y и переносим его параллельно x.

Результат - треугольник наклонен и на оси x.

2. Рассмотрим последовательность Перемещение->Поворот

2.1 OpenGL. Преобразование системы координат - Перемещаем систему координат параллельно x , и поворачиваем вокруг O' , рисуем объект.

Результат - треугольник наклонен и на оси x.

2.2 Преобразование объекта. Перемещаем объект параллельно оси x, поворачиваем вокруг O.

Результат - треугольник наклонен и вверху.