 |
 |
|
|
|
|
|
|
|
2. Логика 2.1 Проекции
Лучше один раз увидеть, чем сто раз услышать. Чтобы изучать 4D-пространство надо посмотреть сначала чего-нибудь этакого четырехмерного: фигуры, например. Но как? Начнем применять аналогии. Найдем различия в ощущении трехмерных объектов нами и 2D-Сашей. Вот наши Саша и Маша.
А вот трехмерный объект.
Вообще-то это двумерное изображение на экране... Стоп! То что нам и надо. Будем использовать проекции. Та-а-ак.... Маша ушла, а Саша остался разбираться с 3D. Мы уже добавили третью ось, к его двумерному пространству.
|
|
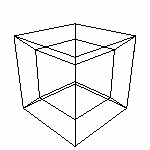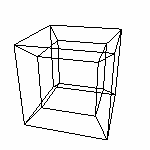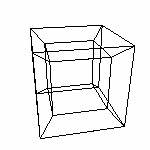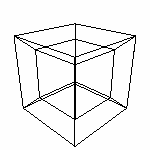
А вот и трехмерный куб. Штриховые линии, это для нас, чтобы оценить его положение. Пока это только для нас.
Покажем куб Саше, то бишь спроецируем его на плоскость.
Синий квадрат - это куб, спроецированный на плоскость. Саша понял, но для него мало информации. А вот, что именно понял Саша, важно для нас. Александр видит двумерный объект. Чтобы обозреть его весь, ему необходимо обойти его со всех сторон. Этот объект Саша называет квадратом.
|
|
Давайте попробуем расположить куб по другому, повернем влево..
...и спроецировать заново...
Саша видит плоскую (плоскость для него - Родина :-) фигуру. Прямоугольник с двумя внутренними отрезками. Но мы то знаем, что он еще видит не все.
|
|
Попробуем сделать еще красивее: поднимем переднюю грань. (цветом выделено, чтобы увидеть положение куба: передняя сторона выше и правее задней)
И проецируем...
|
|
Теперь отдельно покажем проекцию
Это очень ВАЖНО. Хоть мы и получили, казалось бы, знакомое изображение (так рисовали куб еще за долго до появления понятия "проекция"), но давайте посмотрим на него глазами Саши и подумаем его мыслями. Это шестиугольная фигура, из шести внешних отрезков и шести внутренних. Те отрезки, которые в 3D оригинале не пересекались (например, переднее левое ребро и заднее верхнее) на проекции пересекаются (именно пересекаются а не накладываются, это ведь видит Саша). Чтоб увидеть все линии проекции ему необходимо будет строить эти линии ПОЛУПРОЗРАЧНЫМИ!. Дальше больше. Он понимает, что математически 3D-куб - это фигура, где все углы прямые! А получил фигуру, где некоторые углы явно отличаются от 90 градусов. И всякие другие мысли... Теперь по аналогии вывод для наших изысканий. Можно строить трехмерные проекции четырехмерных тел, но надо научится ПРАВИЛЬНО понимать, что мы получаем. Учитывать, что после проекции "правильной" 4D фигуры будет выглядеть "неправильно" ("правильные проекции" не столь информативны). Мы, так же как и Саша, не сможем увидеть весь объект сразу со всех сторон. Для изучения нам потребуется поворачивать его, или самому ходить вокруг. Так же надо сделать поверхность полупрозрачной или исследовать каркас проекции.
|
|
И это еще не все. В данном случае мы использовали
параллельную проекцию, с углом проецирования 90 градусов, то есть
параллельно "новой" третьей оси. В таком варианте новая
ось проецируется в точку. Чтобы Саше увидеть третью ось, необходимо
использовать параллельное проецирование, но с углом наклона. Так
делаем и мы, когда хотим изобразить третью ось на плоскости. Само
изображение Александра на картинках с тремя осями это и есть
параллельная косоугольная проекция. |
|
|
|
|
|
|
|
©2007 AnCoRecords "d'Amateur: Записки 4D любителя" E-mail автору |
|
|
|









