Назад Проекции

Далее Максимальный куб

2.2 Учимся смотреть проекции.

Лучше один раз пощупать, чем сто раз увидеть. Мужики меня поймут
(народная поговорка, Second Edition.)

Мы использовали так называемую параллельную проекцию, с углом проецирования 90 градусов к плоскости (ортографическая проекция). На следующем рисунке это направление обозначено вектором n

Видно что n параллелен третьей оси, и значит перпендикулярен родной Сашиной плоскости. Это не есть лучший вариант.

Например, возьмем трехмерную систему координат (для удобства используем привычные обозначения осей)...

и спроецируем на плоскость

При таком способе третья ось проецируется в точку. Для того, чтобы увидеть проекцию оси необходимо изменить угол проецирования, то есть изменить вектор n (такая проекция называется косоугольной).

Например, так

Теперь построим трехмерную систему координат

...и спроецируем ее на плоскость, чтобы посмотреть будет ли видна третья ось ...

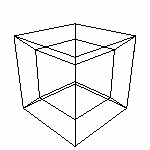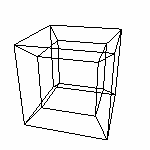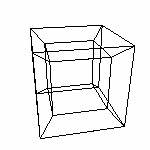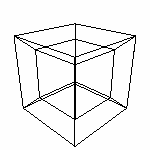
Важно. Опять же хочу напомнить: проекция это ПЛОСКАЯ ФИГУРА. 

Саша видит фигуру состоящую из трех векторов. Как же ему понять, что в оригинале они все перпендикулярны? Да ни как! В его понимании нет ТРЕТЬЕГО перпендикулярно вектора. Остается одно: просто ВЕРИТЬ в это. И второе: не забывать ВЕРУ при исследовании полученного результата.

Но это опять же не все. Как вы видите, положение осей x' и y' изменилось. В данном случае вектор n направлен вправо (по x на +1) и вверх (по y на +3) и обратно направлению новой оси (по z на -2). И при таком направлении проекции меняется положение проецируемых точек. И поэтому точка с координатами (1,1,2) проецируется в точку (2,4). То есть просто отбрасывать третью координату можно только при ортографической проекции. А при косоугольных необходимо рассчитывать по определенной формуле (см. далее в разделе Математика). Сейчас же, используя аналогию, можно сказать, что для того чтобы нам увидеть проекцию четвертой оси, необходимо использовать косоугольную проекцию четырех осей на трехмерное пространство.

Примечание. Вы часто встречались с проекциями: например, тень на стене (плоскости) от чего-либо. А вектор направления проекции можно "с-аналагировать" с фонариком (совершенный глагол от существительного "аналогия") . Правда, в данном случае мы имеем перспективную проекцию. Но при в принципе перспективными искажениями можно пренебречь.

Здесь можно скачать динамическую модель проекции трехмерных объектов на плоскость. Обратите внимание на то, что правильно подобранный вектор проекции влияет на "удобо-читабельность" результата. Постарайтесь научится различать: где объект и где его проекция. Ведь выглядят они одинаково, потому что по сути на мы видим проекцию  трехмерной модели на (плоский) экран (а в этой модели 3D-объект проецируется на плоскость). Но для понимания предмета придется принимать эти условности и учиться "правильно смотреть".

Вывод для 3D проекции 4D.

1. Для получения более информативного проекции 4D фигуры на 3D пространство необходимо использовать параллельную косоугольную проекцию.

2. Точки с нулевой четвертой координатой проецируются сами в себя.

3. При условии ненулевой четвертой координаты, мы будем получать смещение трех "реальных координат"  (подробнее в разделе Математика).

Дополнение.

1. Важно выбрать удачный вектор проекции. Например, на следующем рисунке вектор проекции (1,1,1) не самый лучший для просмотра проекции куба.

Также и при получении проекции, например, гиперкуба, надо будет найти удачный вектор.

Назад Проекции

Далее Максимальный куб

©2007 AnCoRecords   "d'Amateur: Записки 4D любителя"    E-mail автору