Назад Учимся смотреть проекции

Далее Четырехмерный куб

2.3 Максимальный куб

 Дайте мне таблеток от жадности. Да побольше, побольше...

Все знают что такое куб: трехмерный объект состоящий из шести квадратов пары которых параллельны осевым плоскостям.

Для дальнейших исследований пригодится понимание, что квадрат является двумерным кубом, а отрезок, соответственно, одномерным.

Почему именно куб? Потому. Куб является фигурой, которая как бы "повторяет" пространство, его свойства. Совокупность кубов заполняет пространство, как мозаика. Объем (а в общем случае n-размер) вычисляется в кубах (соответствующей размерности). Поэтому считаю, что право быть первой изучаемой фигурой при изучении пространства куб заслужил.

Как говорилось выше, кубом в соответствующих пространствах можно назвать и квадрат, и отрезок, и даже точку (для 0D пространства). Но тот же самый квадрат присутствует и в трехмерном пространстве. Поэтому считаю необходимым ввести понятие Максимального куба.

Максимальный куб -  куб размерности самого пространства.

Может и не самое лучшее определение. И вообще оно нужно тут только для начала. И мне думается каждый человек интуитивно понимает, про что тут идет речь.

 Максимальный куб.

Начнем с определений. (они пригодятся для записи формул в компактном виде)

Определения
1. Pr(n) – n-мерное пространство.
Pr(0) – точка.
Pr(1) – прямая.
Pr(2) – плоскость.
Pr(3) – пространство.

2. Cube – сот-с-с-тна куб.
Cube(n) – n-мерный куб.  n-куб.
Максимальный куб – n-мерный куб в n-мерном пространстве.
Cube(0) – точка. Максимальный для 0-мерного пространства.
Cube(1) – отрезок. Максимальный для 1-мерного пространства.
Cube(2) – квадрат. Максимальный для 2-мерного пространства.
Cube(3) – наш привычный 3-мерный куб. Максимальный для 3-мерного пространства.
3.Граница – граница объекта. Для 3D-куба это вершины, ребра, грани.
Gr(n) – n-мерная граница. n-граница.
Gr(0) – вершина
Gr(1) – ребро
Gr(2) – грань
Gr(3) – куб (сам куб является своей границей).

Дальше для пояснения действий используются различные цвета.

   - черный - оси пространтсва

   - синий - исходные данные

   - желтый - скопированные исходные данные

   - красный - соединение исходных данных и скопированных

Займемся построением. Начнем с ноль-мерного пространства.

Дано. 0D куб - точка.

Задача построить 4D-куб.

Будем действовать последовательно.

1. Построение одномерного куба (отрезка)

Добавили одно измерение.

На расстоянии 1 в новом измерении возьмем копию предыдущего Cube. Т.е. Cube(0). И соединим их, получив Cube(1) - состоящий из двух точек и одного отрезка.

2. Построение двумерного куба (квадрата)

Добавили одно измерение.

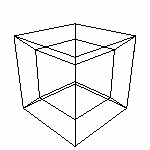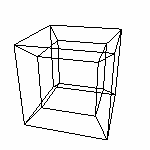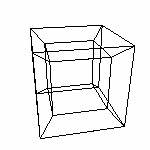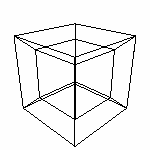
На расстоянии 1 в новом измерении возьмем копию предыдущего Cube. Т.е. Cube(1). И соединим их, получив Cube(2) - состоящий из четырех точек,  четырех отрезков и одного (с-с-стсвн-на) квадрата.

Добавили одно измерение.

На расстоянии 1 в новом измерении возьмем копию предыдущего Cube. Т.е. Cube(2). И соединим их, получив Cube(3) - состоящий из восьми точек,  двенадцати отрезков, шести квадратов и одного (конечно же) куба.

Исходя из хода построения, можно найти зависимость количество границ (точек, ребер, квадратов) от предыдущего построения.

Разберемся, что происходило.

Для этого надо отметить, что граница с размерностью пространства, является самой фигурой, и, соответственно, присутствует в количестве 1. Например, квадрат является своей же границей. И можно говорить, что в квадрате (как в фигуре) один квадрат (как граница).

Допустим у нас есть Cube(n) (для примера возьмем n=1, отрезок) и мы строим Cube(n+1). В нем g штук границ размерности (n-1) (точки - 2 штуки) и одна (всегда одна) граница размерности n (сам отрезок). При построении они скопировались, то есть их количество умножается на 2 (и количество точек, и количество отрезков). Соединяем мы их границами размерности n, и их по количеству столько же, сколько было границ размерности (n-1) (количество соединяющих отрезков).  

Отсюда получаем формулу

Количество Gr(n) в Cube(n) равно сумме удвоенного количество Gr(n-1) и количества Gr(n) в Cube(n-1). Не сложно доказать, что количество Gr(n) в Cube(m) равно сумме удвоенного количество Gr(n-1) и количества Gr(n) в Cube(m-1) (при m≥n).

Обозначим через Kol(m,n) это самое количество Gr(n) в Cube(m) (количество границ размерности n  в кубе размерности m). Тогда формула имеет следующую запись

 Kol(m,n)=2* Kol(m-1,n) +Kol(m-1,n-1);

Отсюда имеем таблицу Расчета количество границ в кубе.

Таблица 2.1

Эта же Таблица в формате Excel с установленными формулами.

Есть занимательные закономерности, видные в рассчитанной нами таблице и связь с  треугольником Паскаля. На рисунке синим цветом выделены номера и направление "линий просмотра" (L).

Назовем L(g,k) - k-тый элемент в линии номер g

В таблице 2.1 определим диагонали

1 - при m=n

2 - при m=n+1

3 - при m=n+2

и вообще

p - m=n+(p-1)

после несложных рассуждений получаем:

Например.

Kol(6,4)=4*15=60

Kol(3,2)=2*3=6

В частности отсюда следует, что Kol(m,m)=1 (сама фигура является своей собственной границей) и  Kol(m,0)=2^m (количество точек равно 2 в степени размерности куба, опять же из-за копирования)

Назад Учимся смотреть проекции

Далее Четырехмерный куб

©2007 AnCoRecords   "d'Amateur: Записки 4D любителя"    E-mail автору