Назад Построение модели пространства

Далее Математика

2.8 Трехмерная проекция четырехмерного пространства

Трезвый конному не пеший.

(здесь это очень кстати)

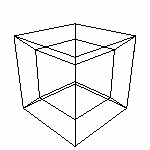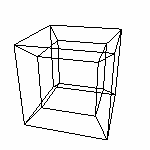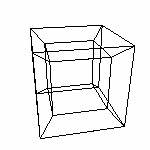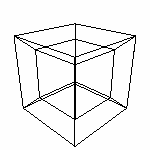
  Мы построили 4D-Пространство и разобрались с его основными свойствами, мельком взглянули на гиперкуб, выявили способы просмотра четырехмерных фигур. Этого должно хватить чтобы начать взаимодействие с четырехмерными объектами.

  Как мы уже выяснили, для изучения 4D-фигур можно использовать их трехмерные проекции на трехмерное пространство.

ВАЖНО. Так как мы начинаем "общаться" с четырехмерными объектами, хотелось бы отметить следующее:

То, что мы будем видеть это проекция того, о чем мы "говорим". И надо смотреть на это как на проекцию, со всеми вытекающими от сюда последствиями: координаты смещаются, формы изменяются и т.д.

А видеть мы будем вот что

 (прочитайте по строкам, попробуйте сначала без "в скобках")

 двумерную проекцию (на экране)

 трехмерной модели (максимум того, что мы можем обозреть)

 трехмерной проекции

 четырехмерного "происходящего".

Учтя это, улавливать разницу между тем, что мы имеем в виду под названием "проекция" и что мы считаем "реальным" объектом.

  Примечание. Все изображения помеченные "MP" получены с помощью расчетов, используя математический аппарат расчета 3D-проекций 4D-объектов, описанный далее в разделе Математика. Но смотреть непривычные изображения (читай "двумерные проекции") трехмерного пространства довольно таки тяжело, с непривычки. Поэтому рядом с каждым таким изображением есть ссылка на файл (с помощью которого это изображение было получено), в котором можно посмотреть все в динамике (3D "номер файла"). Весьма советую.

  Как уже говорилось, (далее извините) смотреть проекцию при  перпендикулярном (к области проецирования) направлении проекции дело малозанятное: просто отбрасывать последнюю координату не интересно. Мы будем использовать косоугольную параллельную проекцию.

ВАЖНО! Как и при проецировании на плоскость в нашем случае важно найти УДАЧНЫЙ вектор проекции.

  Вектор n(x,y,z,q) - направление проекции, в данном случае это четырехмерный вектор

  точка L(x,y,z) - точка "взгляда", которым мы смотри на проекцию.

  Пояснения к рисункам:

Цветами (RGBV) выделены значимые элементы рисунка.
Красный - Red - X
Зеленый - Green - Y
Синий - Blue - Z
Фиолетовый - Violet - Q (чтобы точно не перепутать с направлением в трехмерном пространстве, на конце его не стрелка, а шарик)
Эти же цвета, но тонкие линии - соединительные линии, от Q до оси и потом до O.

При запуске программы открывается два окна: одно с изображением, другое - консольное. Во втором окне может выводится дополнительная информация.

Q projection vector
4D Vector (x,y,z,q) - четырехмерные координаты вектора n
3D Projection (x,y,z) - проекция оси q на трехмерное пространство.

Eye (x,y,z) - координаты точки взгляда L

  Ну начнем...

  Спроецируем 4D-пространство на 3D.

n(1,1,1,1)       L(-1.6,5,2)

MP3D (#1)

 В программе есть возможность управлять вектором проекции.

ПОМНИТЕ!

Фиолетовый отрезок - это НЕ ВЕКТОР ПРОЕКЦИИ. Это проекция оси q. От изменения угла проецирования зависит проекция это оси. Но управлять вы будете не ей а ВЕКТОРОМ ПРОЕКЦИИ.

 Обратите внимание на особенности поведения проекции q при изменении вектора проецирования. Добейтесь совпадения шарика с одной из осей, определите координаты соответствующего вектора. Аналогии с 3D=>2D тут тоже уместны. Например понятно, почему нельзя добиться совпадения проекции Q с начало координат, меняя только координату q вектора n.

Я думаю, на этом этапе вы уже понимаете, что проекция точки находящейся в нашем трехмерном пространстве (четвертая координата равно нулю) суть сама точка. Нас интересует, как же проецируются точки фигуры, "во вне" (в полном "во вне"). А они будут иметь не те (не совсем те) три координаты, что и оригинал.

Назад Построение модели пространства

Далее Математика

©2007 AnCoRecords   "d'Amateur: Записки 4D любителя"    E-mail автору