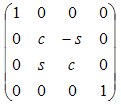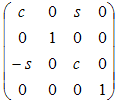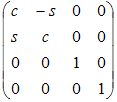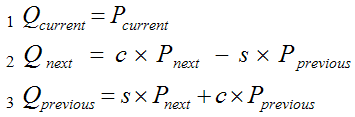 |
 |
|
|
|
|
|
|
|
3. Математика 3.1 Трехмерные аффинные преобразования В греческом зале, в греческом зале... |
|
На уровне этой статьи считается, что вы в курсе аффинных преобразований, и понимаете что матрица это не только генератор энергии для Великого Механизма (трилогия Matrix). Для начала советую ознакомится с главами Матрицы и Аффинные преобразования. |
||
| Трехмерные
аффинные преобразования - состоят из тех же основных видов, что
и двумерные. Но имеет смысл привести их и поиграть в игру найдите
десять отличий. Перемещение
Масштабирование
Сдвиг
Поворот Поворот (он же "вращение") на угол w c=cos(w). s=sin(w) Вокруг оси x от y к z.
Вокруг оси y от z к x.
Вокруг оси z от x к y.
Как видно в повороте вокруг y минус стоит у нижнего синуса, а в остальных матрицах минус у верхнего синуса. Это не означает, что это вращение «неправильное». Объяснение №1. (При использовании [Л1]). Рассмотрим три оси x,y,z в циклическом
порядке: x→y→z→ x→y,… и т.д. Если мы исследуем вращение вокруг
какой-нибудь «текущей» (current) оси (x,y или
z), то мы можем указать «предыдущую» (previous)
и «следующую» (next) оси. Если, например,
текущей является ось x, то предыдущая –z, а следующая –y. Можно
доказать, что при такой системе названий во всех трех видах
поворотов используются одни и те же уравнения:
Немного поясню. Понятия «текущий», «следующий» и «предыдущий» применяются к соответствующим координатам точки относительно оси вращения. Конец цитирования [Л1] Объяснение №2 (более наглядное) У каждой матрицы есть характерный "рисунок". Этим словом я назвал схематическое взаимо-место-расположения значимых элементов. Например, у матрицы вращения вокруг x и z рисунок одинаковый:
А в y-матрице
Если разобраться почему меняется рисунок, сразу станет понятно "измена" минуса у синуса. Дело в том, что существует циклическая последовательность осей x→y→z→ x→y,… и т.д. Следовательно, есть циклическая последовательность матриц преобразования. И следующую матрицу можно получить из предыдущей следующим образом. Следующая матрица получается "перемещением" к
концу строк и столбцов матрицы. Начнем вращения вокруг x (таблица слева направо, сверху вниз) |
|
|
Смещаем вторую строку на третью, а третью перемещаем на первую и получаем... |
|
|
|
Смещаем второй столбец на третий, а третий столбец перемещаем на первый и получаем.. |
|
| Получили y-вращение. Таким же образом из y-вращения можно получить z-вращение, и после вернуться к вращению вокруг оси x. Как видно минус у синуса вовсе и не прыгает. Он всегда на своих местах. Есть еще и объяснение №3. Еще более нагляднее, но уже в четырехмерном пространстве. Разобрались? Тогда можно переходить к четырехмерным аффинным преобразованиям.
|
|
|
|
|
|
|
|
©2007 AnCoRecords "d'Amateur: Записки 4D любителя" E-mail автору |
|
|
|