 |
 |
|
|
|
|
|
|
|
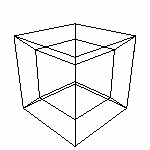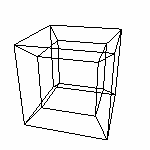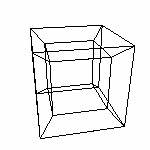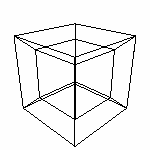
4.
Модели 4D 4.3 Тетраэдр и Гипертетраэдр. Тетраэдр Тетраэдр - трехмерный треугольник. Фигура состоящая из четырех треугольников. Для наших нужд нет необходимости брать правильный тетраэдр. Будет вполне достаточно взять с вершиной в начале координат и ребрами на осях.
Фигура описывается просто. Три треугольника в основных плоскостях и один (на рисунке ближайший к нам) соединяющий точки на осях. Файл для Transformator4DV1
1 Конечно, прорисовав первые три треугольника мы получим четвертый треугольник автоматически. Но в данной статье важно определится что у тетраэдра четыре треугольника. Определим Тетраэдр(t) - тетраэдр с вершиной в начале координат и вершинами (t,0,0), (0,t,0), (0,0,t). В данном случае (на рисунке выше) мы построили Тетраэдр(1). Все остальные можно получить аффинными преобразованиями. Тетраэдр определяется четырьмя точками, поэтому для облегчения дальнейших построений создадим подпрограмму (например, в Excel) расчета последовательности соединений точек тетраэдра. Например вот (здесь уже четвертый треугольник не прорисовываем) Гипертетраэдр Вершины этой фигуры 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 Пять штук. обозначим эти точки соответственно O,X,Y,Z,Q Каждые четыре определяют тетраэдры, из которых и состоит Гипертетраэдр. 1. O,X,Y,Z (наш трехмерный) 2. O,X,Y,Q (тоже трехмерный, но протяженный в четвертое измерение) 3. O,X,Z,Q (как и 2.) 4. O,Y,Z,Q (как 2. и 3.) 5. X,Y,Z,Q внешний Напишем файл для Transformator4D используя файл Excel для расчета.
Видны все пять составляющих тетраэдров 1 - по "нашим" трем осям 2,3,4 - по две "наши" оси и ребро на оси q (фиолетовый отрезок). 5. Объединяет точки на осях. А он действительно внешний.
|
|
|
|
|
|
|
|
|
|
©2007 AnCoRecords "d'Amateur: Записки 4D любителя" E-mail автору |
|
|
|

