 |
 |
|
|
|
|
|
|
|
4.
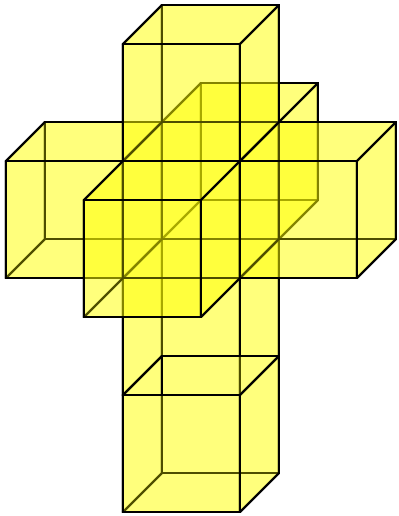
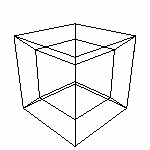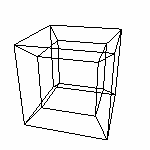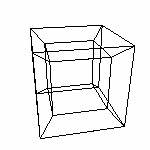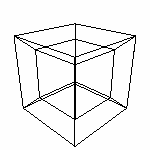
Модели 4D 4.2 Развертка гиперкуба. Развертку мы уже рассматривали в разделе Логика. Но теперь после изучения аффинных преобразований, мы знаем как ее собрать в гиперкуб - надо повернуть все кубы развертки на 90 градусов относительно соединения с другим кубом. (конечно, за исключением внутреннего куба, его никуда поворачивать не надо). Напомню развертку
Все кубы должны заворачивать в сторону четвертого измерения. Опишем направления поворотов. Для начала определится с номерами кубов и координатными осями.
Средний куб не двигается, поэтому мы его трогать не будем. И начнем движуху. Напомню, у нас есть куб с вершиной в начале координат - средний куб, и все построения мы будем начинать с него. Куб №1 Смещение (-1,0,0,0) Так как грань у него в плоскости yz, вращать будем в напралении xq. Из построения развертки куба выведем направление поворота. от q к x (так как находится в "минусе"). Поворот на 1 градус (0,0,-1,0,0,0) (Исходя из xy xz xq yz yq zq). Куб №2 Поворот вокруг плоскости xy значит от z к q. (0,0,0,0,0,1) Смещение (0,0,1,0) Куб №3. Поворот (0,0,1,0,0,0) Смещение (1,0,0,0) Куб №4. Смещение (0,0,-1,0) Поворот (0,0,0,0,0,-1) Куб №5 Поворот (0,0,0,0,1,0) Смещение (0,1,0,0) Куб №6 Смещение (0,-1,0,0) Поворот (0,0,0,0,-1,0) Куб №7 Смещение (0,-1,0,0) Поворот (0,0,0,0,-1,0) Смещение (0,-1,0,0) Поворот (0,0,0,0,-1,0) Для удобства нам можно сделать куб одним полигоном. Описание куба одним полигоном Примерно вот таким образом (сначала низ, и вернемся в точку 0,0,0,0, после поднимаемся наверх и описываем верхнюю грань)
18 // количество точек 0 0 0 //цвет 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 1 1 0 0 1 0 0 0 1 0 1 0 1 1 1 0 1 0 1 0 0 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 //это левый рисунок, а теперь правый 0 1 0 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 0. Будем использовать это в программе под названием Куб, для использования нужно будет просто заменить куб на приведенную выше последовательность чисел.
Файл программы для Transformator4DV2. (комментарии не являются частью файла) //Начало 1 //замкнутые полигоны 1 1 1 1 //вектор проекции 8 //количество полигонов Куб 0 //количество преобразований Куб 2 //количество преобразований 2 1 -1 0 0 0 6 1 0 0 -1 0 0 0 Куб 2 6 1 0 0 0 0 0 1 2 1 0 0 1 0 Куб 2 2 1 1 0 0 0 6 1 0 0 1 0 0 0 Куб 2 6 1 0 0 0 0 0 -1 2 1 0 0 -1 0 Куб 2 6 1 0 0 0 0 1 0 2 1 0 1 0 0 Куб 2 2 1 0 -1 0 0 6 1 0 0 0 0 -1 0 Куб 4 2 1 0 -1 0 0 6 1 0 0 0 0 -1 0 2 1 0 -1 0 0 6 1 0 0 0 0 -1 0
Проверим.
1
2
2
2
Гиперкубик Рубика И вот вам "домашнее задание". Сможете представить себе четырехмерный кубик Рубика? Если сможете описать его свойства: все "свободы вращения", ориентацию, количество составляющих гиперкубиков - значит вы хорошо усвоили материал, можно начинать гордиться! В Интернете есть программка для сбора ГиперКубика-Рубика. Прикольно! |
|
|
|
|
|
|
|
©2007 AnCoRecords "d'Amateur: Записки 4D любителя" E-mail автору |
|
|
|