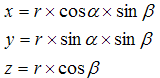Назад Модель аппроксимации Сферы

Далее d'Amateur: Это не конец

4.4 Гиперсфера.

    Для начала можете посмотреть на это Гиперсфера на Wikipedia.org

  Гиперсфера - четырехмерная сфера. Совокупность точек в четырехмерном пространстве на одинаковом расстоянии от одной точки, называемой центром гиперсферы. Уравнение в полярных координатах

Радиус можно опустить приравняв его к единице.

(5.1)

а теперь используем уравнение сферы

(5.2)

Если sin γ в (5.1) - воспринимать как радиус в (5.2), а cos γ - как смещение сферы (5.2)по оси q , то можно сделать вывод, что аппроксимация гиперсферы состоит из сфер с радиусом sin γ и смещением по q на cos γ. Эти сферы являются параллелями гиперсферы. (!!!). Чего то мы быстро их нашли, оставим их на сладкое.

Есть ли полюса? Есть! При γ=0 и γ=180. Координаты полюсов (0,0,0,±1).

Другие пересечения с осями. Назовем их ключевыми точками.

(±1,0,0,0) при α равном 0 или 180 градусов, и β=γ=90 градусов.

(0,±1,0,0) при α равном 90 или -90 градусов, и β=γ=90 градусов.

(0,0,±1,0) при α равном 0, и β равном 0 или 180 градусов, и γ=90 градусов.

Мы определились, что параллелями в гиперсфере являются сферы. А что же будет меридианами? Как раз тут нам помогут ключевые точки. Ведь в сфере два меридиана проходят через полюса и точки пересечения сферы с осями. Мы так же сделаем и в нашем случае. Для начала найдем лини проходящие через полюса и ключевые точки. Но это означает, что меридианы гиперсферы - это окружности! ДВУМЕРНЫЕ! А параллели ТРЕХМЕРНЫЕ! Не все так просто, все зависит от нашего желания... Да и в предыдущей статье  я и обратил ваше внимание на разную смысловую нагрузку параллелей и меридианов.

Меридианы гиперсферы.

Сначала, чтобы осознать закономерности, составим алгоритм нахождения ключевого меридиана (проходящего через ключевую точку) для сферы. Их там 2 штуки.

Введем обозначения:     a=α                  b=β

1. Ключевая точка на x (±1,0,0). α= 0

Цикл b от 0 до 360    x=sin b    y=0  z=cos b

Соединяем точки (sin b , 0 , cos b)

2. Ключевая точка на y (0,±1,0). α= 90

Цикл b от 0 до 360   x=0    y=sin b  z=cos b

Соединяем точки (0 , sin b , cos b)

Теперь создадим 3 меридиана Гиперсферы проходящих через ключевые точки.

Обозначения a=α                  b=β                       g=γ

1. Ключевая точка на x (±1,0,0,0)

a=0,    b=90

Цикл g от 0 до 360    x=sin g   y=0    z=0   q=cos g

Соединяем точки (sin g , 0 , 0 , cos g)

Ключевые точки при g=90  =>  (1,0,0,0)   и    g=270  =>  (-1,0,0,0)

2. Ключевая точка на y  (0,±1,0,0)

a=90,    b=90

Цикл g от 0 до 360    x=0   y=sin g    z=0   q=cos g

Ключевые точки при g=90  =>  (0,1,0,0)   и    g=270  =>  (0,-1,0,0)

3. Ключевая точка на z  (0,0,±1,0)

a=0,    b=0

Цикл g от 0 до 360    x=0   y=0    z=sin g   q=cos g

Ключевые точки при g=90  =>  (0,0,1,0)   и    g=270  =>  (0,0,-1,0)

и у всех ключевых меридианов при g=0 или g=180 получаем полюса (0,0,0,±1).

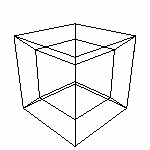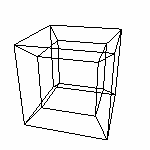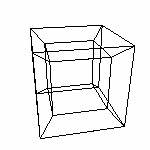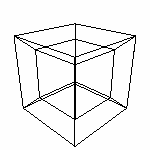
При реализации этого алгоритма расчета можно получить следующий рисунок

(при векторе проецирования (1,1,1,1))

Стрелками указаны полюса. При ортографической проекции (0,0,0,1) мы получим три взаимно перпендикулярных отрезка с концами как раз в ключевых точках.

Нельзя сравнивать эти три окружности в четырехмерном пространстве с тремя окружностями следующего представления сферы.

Здесь два меридиана и одна ПАРАЛЛЕЛЬ! А там все три - МЕРИДИАНЫ лежащие в трех ПЕРПЕНДИКУЛЯРНЫХ плоскостях.

Расчет меридианов гиперсферы довольно таки прост: три вложенных цикла по трем углам. Во внутреннем цикле рассчитываются координаты. И соединяются.

Файлов аппроксимации гиперсферы для Transformator4D нет, так как там большое количество полигонов и точек. Поэтому созданы отдельные программы для представления проекции Гиперсферы.

Вот тут, например, различные представления аппроксимации гиперсферы меридианами  (5.3). В имени файла последние четыре литеры указывают на порядок взятия координат исходя из уравнения (5.1) Например, XYZQ - обозначает такой же порядок. А XYQZ - указывает на то, координаты q точек рассчитывается по третьей строке уравнения, а z по четвертой.  Как видите, полюса находятся на оси обозначенной последней буквой.

Все остальные виды, когда полюса находятся на осях x и y отличаются от z только ориентацией.

Так все-таки: меридианы гиперсферы двумерные или трехмерные? Вообще-то это как посмотреть. Исходя  того что гиперсфера описывается тремя углами в полярных координатах, можно назвать меридианом трехмерную фигуру образованную двумя углами. А третий будет "множителем"...

  Попробуйте провести эксперимент. Запустите GiperSphereXYQZ и измените координату x либо y вектора проекции на довольно таки большое значение. Отодвиньте камеру, чтобы вам было видно всю проекцию. Вы сразу увидите затемненные участки. Приглядитесь...

Вот тут их еще не видно...

И вот они! Позвольте представить! Трехмерные  меридианы четырехмерной сферы! (справа аналог для проекции меридианов трехмерной сферы)

(5.4)

Это двумерная проекция меридианов трехмерной сферы с центром в плоскости проецирования при векторе проекции с маленьким углом от плоскости проецирования. В центре окружность - меридиан принадлежащий плоскости, поэтому он не искажается.

Слева, в проекции гипермеридианов тоже есть сфера в центре без искажений. Этот меридиан лежит в ПРОСТРАНСТВЕ проецирования, поэтому не искажается.

Чтобы отчетливее себе представить себе эти 3D-меридианы, вот вам на засыпку...

Когда мы строили аппроксимацию сферы, мы договорились называть меридианами окружность, а не дугу. То есть при построении брали все 360 градусов, а если взять половинку, 180? Так у нас не один угол а два!

(далее в примерах берется последовательность (из уравнения 5.1) XYQZ а управление вектором проекции x,y,z,q - Q/A,W/S,E/D.R/F)

1. Представление одного мердиана (5.5) предыдущий рисунок-скриншот.

Параметры:  α от 0 до 360                β=54                       γ от 0 до 360 (все в градусах)

2. Следующий вид того же меридиана

С параметрами:  α от 0 до 180          β=54                       γ от 0 до 360

Как видите, ушла одна часть.

3. Опять тот же меридиан но при   α от 0 до 360          β=54                  γ от 0 до 180

Пропала половинка!

4. И на последок... α от 0 до 180         β=54                  γ от 0 до 180

Поиграли и хватит.

Вернемся к основному виду из программы 5.5

Хорошо различимы окружности, параллельные плоскости xy. Очень похожи на параллели.

Примечание. Параллели гипермеридиана - окружности в параллельных плоскостях - в программе прорисовываются отдельно. Если взять чистый цикл α,β,γ то изображение состоит из одних меридианов гипермеридиана. Вот так.

Параллели же прорисовываются соединением двух точек при α,β,γ и α+1,β,γ

Вот, например, одни параллели гипермеридиана.

Но вернемся к нашим баранам...

Если приглядеться, можно заметить, что вообще вся фигура состоит из эллипсов. но что это вообще за фигура (5.5)? Для исследования используем еще одно представление меридиана.

А именное вот это. (5.6)

Напомню: вывод о том, что в гиперсфере гиперпараллелями являются обычные сферы. Это хорошо видно из того, что уравнение сферы

(5.2)

А в уравнении гиперсферы

(5.1)

sin γ (5.1) можно считать РАДИУСОМ (5.2), а cos γ - смещением сферы (5.2). (От математики ни куда не деться!)

Так все построение сводится к тому, чтобы перебрать все возможные значения γ. А алгоритм построения сферы у нас уже есть. И формировать гиперпараллели из расчета радиус равен sin γ, а координата центра (0,0,0,cos γ)

Итак, мы увидели, что гиперсфера оказалась не такой простой как сначала нам представлялось.

Назад Модель аппроксимации Сферы

Далее d'Amateur: Это не конец

©2007 AnCoRecords   "d'Amateur: Записки 4D любителя"    E-mail автору