 |
 |
|
|
|
|
|
|
|
3. Математика 3.4 Построение четырехмерного куба |
|
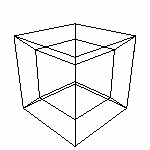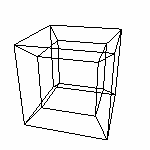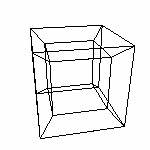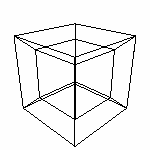
Начнем строить четырехмерный куб, обобщая разработанный в
предыдущей статье алгоритм. Давайте строить гиперкуб. По формуле из главы 2.3 мы знаем, что поверхность гиперкуба состоит из 8 кубов. Теперь найдем этому геометрическое объяснение. у нас четыре оси (x,y,z,q). Имеем вот такие возможные сочетания направляющих для кубов: x,y,z Количество осей определяет количество возможных направлений. Значит и количество комбинации (по 3) направлении равно количеству комбинации осей. Куб определяется тремя векторами, значит мы имеем четыре набора векторов, определяющие четыре куба. А еще четыре куба мы получим "скопировав" полученные, также как копировали в предыдущих построениях. Так как мы вышли в четвертое измерение, необходимо к векторам добавить по координате. Четырехмерный вектор имеет четыре координаты. V(x,y,z,q) Начнем-с... Есть вектор 0 - "начало" гиперкуба, и вектора 1,2,3,4 - направляющие. Куб 1 (0,1,2,3) Теперь скопируем по правилу определенному в предыдущей главе, то есть сместим "начало" на вектор не участвующий в определении куба. Куб 5 (0+4,1,2,3) Координаты я думаю вычислить не сложно... Смотрите тут, если сложно. |
|
|
|
|
|
|
|
©2007 AnCoRecords "d'Amateur: Записки 4D любителя" E-mail автору |
|
|
|