 |
 |
|
|
|
|
|
|
|
3. Математика 3.3 Построение трехмерного куба Повторение - мать учения. |
|
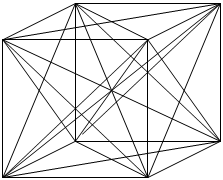
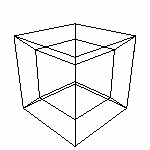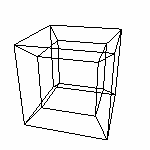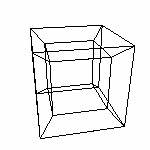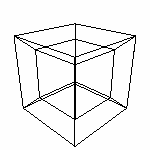
В главе 2.3 Максимальный куб раздела 2. Логика мы строили куб. Но для математических изысканий необходимо определить координаты куба. Как и быстро (и со вкусом) рассчитать? Зачем это нужно? С одной стороны мы можем просто посмотреть на куб и указать все координаты. Но как мы "посмотрим" на четырехмерный куб? Задача этой главы: найти общее решение нахождения координат куба. Координаты не только точек, для прорисовки нам необходимо знать последовательность вершин, которой определяются ребра, грани. Ведь если просто соединить вершины куба всеми возможными способами, мы получим следующее...
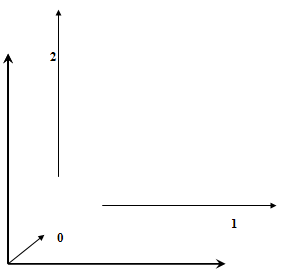
Такой результат я думаю нас не устраивает. А в 4D-кубе так вообще 16 точек и количество соединительных линии будет столь велико, что на 3D-проекции мы увидим черное пятно с белыми проблесками. Разработанный алгоритм построения трехмерного куба в дальнейшем поможет нам при нахождении координат четырехмерного куба. Очень важно понять способ нахождения координат, так как используя аналогичный алгоритм мы в дальнейшем будем строить четырехмерный куб. Выбран именно этот способ, потому что он очень легко программируется, и именно он используется для расчета в представленных программках (динамическая модель) Начнем с того что грани куба являются квадратами. И с начала построим квадрат. Есть три вектора (вместо буквы латинского алфавита для обозначения будем использовать числа: номер вектора).
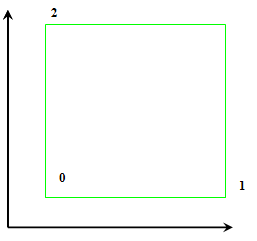
0 - определяет "начало" квадрата 1 и 2 - "направляющие" Мы соответственно должны найти координаты всех точек квадрата
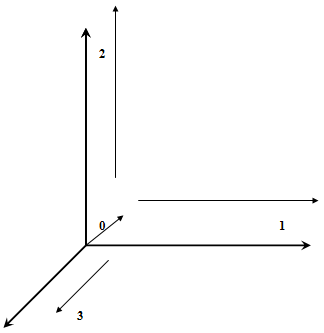
Найдем координаты всех точек с помощью сложения векторов и определим последовательность соединения 0 0+1 0+1+2 0+2 Мы построили квадрат, который определяется тремя векторами. Обозначим его через Квадрат( f , g , h) где f, g, h - вектора определяющие квадрат. Теперь построим куб У нас есть четыре вектора
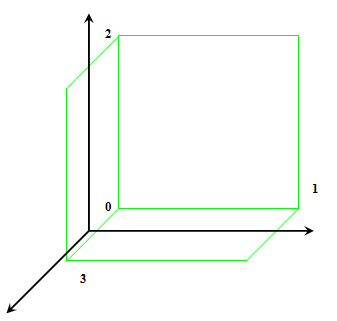
0 - определяет "начало" квадрата 1,2 и 3 - "направляющие" Сразу же можем определить три квадрата Квадрат 1 (0,1,2)
Надо получить еще 3 квадрата Они определяются просто. Уже имеющиеся квадраты копируются по следующему принципу: Квадрат, с направляющими векторами переносится на вектор, который не является для него направляющим (Правило), то есть: Квадрат 4 - Квадрат 1 (0,1,2) переносится на вектор 3 Квадрат 4 (0+3,1,2) Квадрат 5 (0+1,2,3) Квадрат 6 (0+2,3,1)
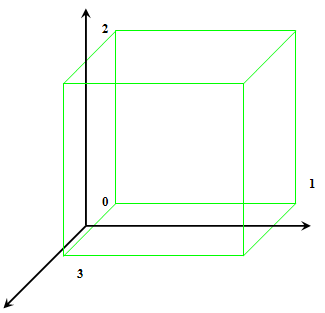
Квадрат 1 (0,1,2) ...и построим куб
|
| Обозначим куб Куб (f ,g, h, j) - куб с началом в f и направляющими g, h и j. На самом деле мы создали алгоритм построения параллелепипеда , так как направляющие векторы могут быть и не перпендикулярны. Для обобщения эти же принципы можно было бы использовать для построения с начала отрезка, потом кадрата из четырех отрезков. Но я думаю на этом этапе это уже лишнее (и грамоздкое), и при желании Вы сможете сделать это сами. Переходим к построению четырехмерного куба! |
|
|
|
|
|
|
|
©2007 AnCoRecords "d'Amateur: Записки 4D любителя" E-mail автору |
|
|
|