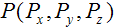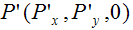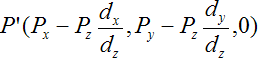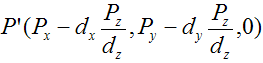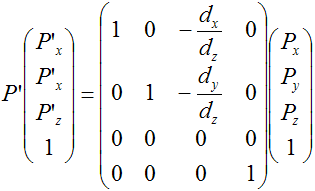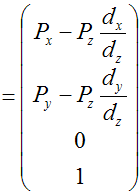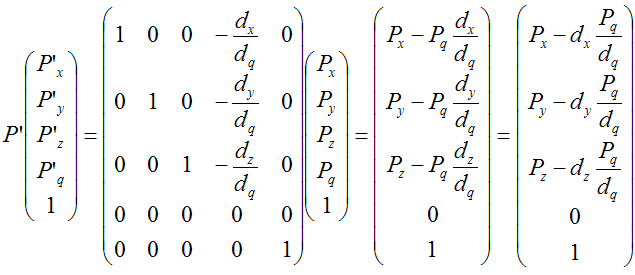 |
 |
|
|
|
|
|
|
|
3. Математика 3.5 И снова проекция Проекция 3D на 2D |
|
Проекция точки в общем случае
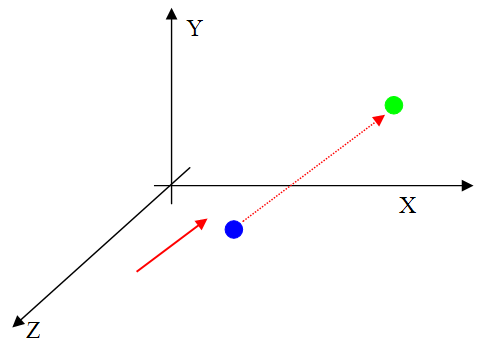
В нашем случае (параллельная проекция) все проецирующие лучи параллельны, и поэтому мы просто указываем направление проецирования с помощью вектора. Чтобы найти формулу нахождения координаты проекции в зависимости от точки оригинала и вектора проецирования можно пойти разными способами. Выберем наглядный способ. Для начала определимся: у нас есть точка в пространстве
мы должны получить точку на плоскости
с помощью вектора
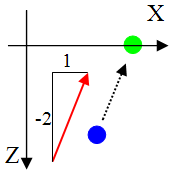
Для примера возьмем вектор d(1,0,-2) - то есть параллельный плоскости xz. При этом векторе проекции P'y=Py. (то есть координата y не меняется)
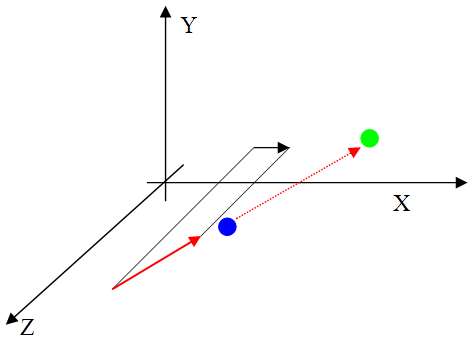
Разберем на части вектор d. Так как он параллелен плоскости zx, то мы его и нарисуем в этой плоскости.
|
||
| Возьмем отношение |
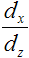 |
|
| Этот показатель равен тангенсу угла между вектором и осью z. Он показывает на сколько смещается координата P'x относительно Px , в зависимости от Pz. В самом деле, чем больше компонента z у точки P, тем больше смещение. | ||
| То есть, чтобы найти x' надо от первоначальной координаты x отнять |
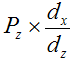 |
|
| после аналогичных рассуждений для y получаем |
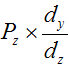 |
|
|
Почему отнять, а не прибавить? Потому что вектор направлен в противоположную сторону относительно направления z. и мы просто компенсируем этот минус. Таким образом получили формулу для получения проекции трехмерной точки на плоскость.
Если записать ее в немного в другом виде виде
то становится видно, что существует определенный коэффициент, определяющий |
| проекцию точки |
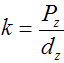 |
|
| как зависимость от третьего измерения | ||
|
Можно записать это в виде произведения матриц
Как видно элемент матрицы (3,3) равен 0 - мы получаем точку с z=0. А значения в третьем столбце определяют аффинное преобразование сдвиг. Таким образом при параллельной проекции координаты образа сдвигаются в зависимости от z-координаты оригинала и вектора d. А также видно, что вектор |
||
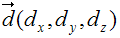 |
и вектор |
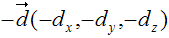 |
дают один и тот же результат |
|
Проекция 4D на 3D После аналогичных рассуждения для проекции точки в четырехмерном пространстве на трехмерное пространство можно получить следующее: |
|||
|
|
| Виден коэффициент, определяющий сдвиг. И он зависит от координаты q оригинала и отношения текущего компонента вектора проекции (x,y,z) к q-координате этого же вектора. |
|
|
|
|
|
|
|
|
|
©2007 AnCoRecords "d'Amateur: Записки 4D любителя" E-mail автору |
|
|
|