 |
 |
|
|
|
|
|
|
|
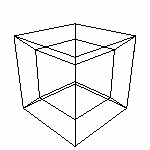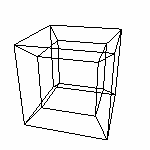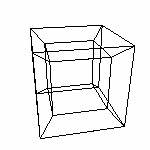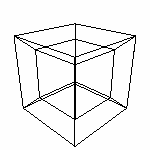
4. Модели 4D Свойства четырехмерных объектов. На этом этапе уже можно с уверенностью говорить о четырехмерных объектах. И поэтому считаю необходимым немного объясниться с 4D. Это нам поможет в наших попытках ощутить четвертое измерение. Поверхность объекта. Что такое поверхность знаю все. Но только для трехмерных фигур. Поверхность в общем случае. Вот это интересно. Например, поверхность куба это шесть квадратов. А поверхность квадрата? Лучшим претендентом на это является совокупность из четырех отрезков-ребер. Про отрезок тоже можно сказать, что поверхность - две его концевые точки, но в нашем понимании поверхность объекта должна быть "связанной", непрерывной. Поэтому, утверждать не берусь. То есть поверхность объекта - это то, что ограничивает объект в пространстве, даже можно сказать содержит внутри. Но можно ли говорить, что поверхность имеет размерность на единицу меньшую размерности объекта. Вряд ли (не знаю как правильно пишется это слово!). Поверхность шара - сфера, не совсем двумерный объект. Поверхность трехмерного объекта - плоская, но "загнутая" в третьем измерении. У сферы "гладко загнута", у куба "угловато". По аналогии с выше сказанным можно сказать, что поверхностью четырехмерного объекта являются трехмерная фигура "искаженная" четвертым измерением. Например для Гиперкуба поверхностью является совокупность восьми кубов. Трехмерных кубов. А квадраты (стороны) этих кубов это тоже самое, что ребра для самого куба. Ни какой количественной характеристики объекта! (Что вам даст длина всех ребер куба?) А для ГиперШара поверхностью является трехмерный объект "завернутый" в четвертом измерении. Это и есть Гиперсфера. Объем Объемом мы называем именно трехмерную количественную характеристику объекта. А для других "nD-объемов" существуют другие названия: площадь для 2D и длина для 1D. А что же такое четырехмерный объем? На примере Гиперкуба. Объем всех составляющих кубов - это категория поверхности. То есть то же самое что площадь поверхности 3D-куба. А 4D-объем? Вот тут нам даже проекции не помогут. Так как это новая (для нас) характеристика именно четырехмерного объекта, и спроецировать ее нельзя. Рассчитать? - Да!. Увидеть? - Нет! Напомню картинку из одного из первых разделов.
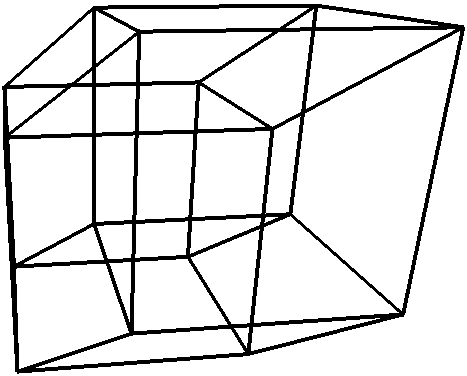
По ощущениям Саши, проекция куба НИ КАК не сообщает ему о части трехмерного пространства ограниченной кубом. В его жизненном опыте нет ассоциаций. Он может попытаться представить себе расположение основных узлов куба. Но у него нет чувства объемности - характеристики третьего измерения. Так же и у нас. Мы можем спроецировать Гиперкуб. И увидеть...
...кучу пересекающихся отрезков. Из отрезков сложим параллелограммы (квадраты). Видим, что одни находятся внутри, другие снаружи. При определенной сноровке можно разглядеть 8 параллелепипедов. Это и есть кубы, составляющие четырехмерную поверхность. То есть это НЕ ГИПЕРКУБ, а его ПОВЕРХНОСТЬ! То есть кубы НЕ ПЕРЕСЕКАЮТСЯ. Они разнесены в четвертом измерении, каждый куб соединяется своими гранями с со всеми шестью соседними кубами. И в совокупности они ограничивают 4D-область 4D-пространства. Например, на этом рисунке видны два куба. На самом деле между ними расстояние равное длине ребра этих кубов (расстояние как и во всех пространствах измеряется в линейных величинах). И так между всеми кубами, видимыми как параллелепипеды. Эти кубы находятся в разных 3D-пространствах. Противоположные кубы в параллельных 3D-пространствах. От каждой точки одного куба, до соответствующей точки другого одно и тоже расстояние (через четвертое измерение) равное длине ребра. В оригинале ТО, ЧТО НАХОДИТСЯ МЕЖДУ НИМИ и есть Гиперкуб! По этой проекции мы можем сделать лишь предположения о действительном положении составляющих. Но, к сожалению, нам не дано прочувствовать весь гиперобъем гиперкуба.. :-( ...К сожалению не дано... Модели В данном разделе будут рассмотрены и построены модели некоторых геометрических примитивов и других геометрических фигур. На них мы все таки попытаемся отдалится от пессимизма предыдущей статьи. Упор будет сделан на использование возможностей программы Transformator4D. |
|
|
|
|
|
|
|
©2007 AnCoRecords "d'Amateur: Записки 4D любителя" E-mail автору |
|
|
|