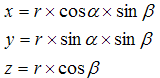Назад Модель Тетраэдра и Гипертетраэдра

Далее Модель аппроксимации Гиперсферы

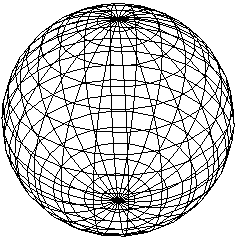
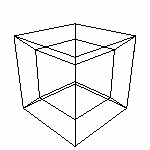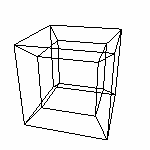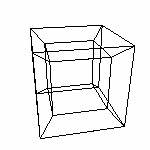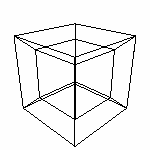
4.3 Сфера.

  На одном из форумов я встретил сообщение: "Я хоть сейчас нарисую вам проекцию сферы!" Конечно, имелось ввиду  что проекция сферы это окружность. Но эта проекция нам ничего не даст. Информативности - ноль! Поэтому предлагаю использовать аппроксимацию сферы.

По словарю Ожегова

АППРОКСИМАЦИЯ, АППРОКСИМИРОВАНИЕ [ лат. approximare приближаться] - математическое приближенное выражение каких-либо величин (или геометрических объектов) через другие, более простые величины.

Нам всем известна аппроксимация сферы - модель глобуса нашей планеты. Есть меридианы, параллели..

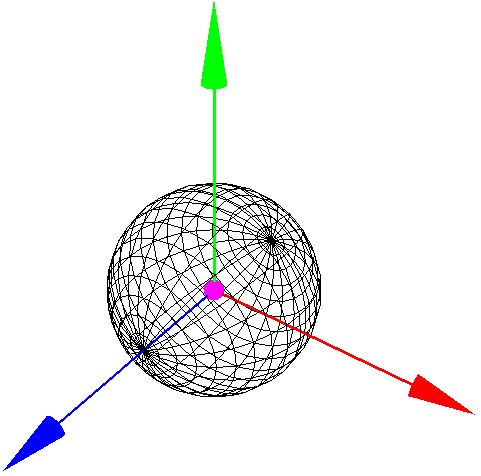
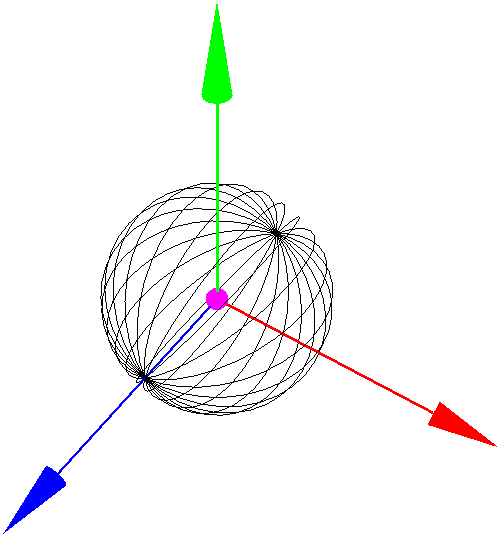
В этой статье будет описан способ построения аппроксимации сферы, на основе которого будет строится аппроксимация гиперсферы (четырехмерной сферы).

Начнем с того, что для нас привычнее именно вид с меридианами и  параллелями. И потому у сферы явна видна главная (general) ось, проходящая через полюса. Сначала сформируем меридианы, потом (именно после меридианов) будем формировать параллели. За главную ось возьмем ось z

Будем использовать общее уравнение сферы в полярных координатах.

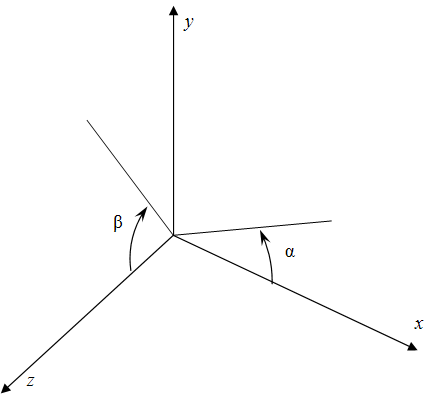
где, r - радиус сферы, α - угол в плоскости xy (от x к y). β - угол от оси z. При этом ось z будет главной.

Сразу разберемся с полюсами. Полюса - точки с координатами (0,0,±1).

Это и понятно, при угле β равном 0 и 180. sin β=0.

А z, как раз 1=cos0 и -1=cos180

Другие пересечения с осями.

(±1,0,0). α= 0 или 180              β=90

(0,±1,0). α=90 или α=-90           β=90

Меридианы

Алгоритм построение меридианов сводится к перебору углов α от 0 до 360, потом внутренним циклом перебор углов β. Потом нахождение по уравнению координат точек. Соединяя их надлежащим образом, мы получаем меридианы. В контексте проекта назовем меридианом всю окружность, а не дугу от полюса до полюса.

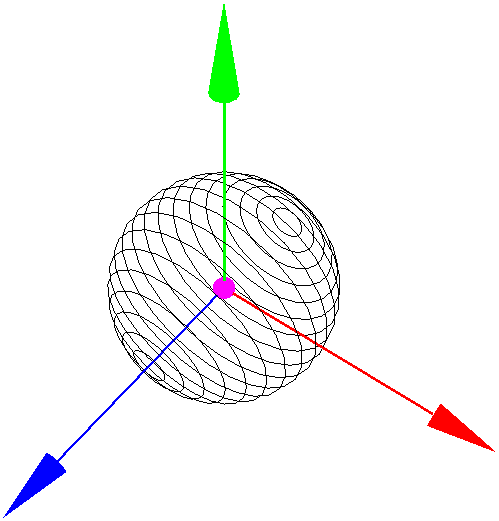
Параллели.

Алгоритм построения параллелей похож. Просто сначала мы пробегаемся по углу β, а внутри этого цикла по углу α.

Соединяя параллели и меридианы получаем аппроксимацию сферы, к которой мы привыкли.

     Программа формирования файла фигуры "аппроксимация сферы"  для Transformator4D обеих версий и примеры файлов расположена на странице

 Файлы программы Transformator4D.

Теперь, как всегда анализ наших действий.

Полюса - две точки сферы при β=-90 и β=90. (β - последний угол)

Меридианы и параллели являются окружностями. Но они несут разную смысловую нагрузку. Хотя бы просто визуально сравнив раздельные представления сферы меридианами и параллелями можно узреть, что параллели в более приемлемом виде представляют сферу, чем меридианы, где сфера похожа на освежеванный апельсин. (хотя может это все субъективно)

Разница между ними очевидна, но не всеми заметна.

Меридианы - окружности одинакового радиуса, пересекающиеся в полюсах.

Параллели - окружность различного радиуса, в параллельных плоскостях.

То есть, сформировав меридианы нам просто надо прорисовать окружности с радиусами, зависящими от угла β. Это важное следствие пригодится при нахождении аппроксимации гиперсферы.

Из моих личных субъективных ощущений - меридианы описывают каркас сферы, а параллели - ее структуру. И, строя сферу, мы на структуру надеваем каркас.

И еще. Мы не использовали понятия радиуса сферы. В данном случае он равен 1,а аффинными преобразованиями мы можем масштабировать его до любого радиуса. (кстати, указывая разные коэффициенты, мы сможем получить эллипсоид). Но потом он нам пригодится.

Назад Модель Тетраэдра и Гипертетраэдра

Далее Модель аппроксимации Гиперсферы

©2007 AnCoRecords   "d'Amateur: Записки 4D любителя"    E-mail автору